How to Know if You Can Have a 3rd Leg of a Triangle
Area of Triangle with 3 Sides
In social club to discover the area of triangle with 3 sides, we use the Heron's Formula. The area of a triangle can be calculated with the help of diverse formulas. The basic formula that is used to notice the surface area of a triangle is ½ × Base × Height where "Base of operations" is the side of the triangle on which the distance is formed, and "Height" is the length of the altitude fatigued to the "Base of operations" from its opposite vertex. However, if the distance of a triangle is non known, and we need to detect the area of triangle with 3 different sides, the Heron's formula is used. This formula was derived by a Greek mathematician known as the Heron of Alexandria. Let u.s. explore the different formulas that are used to find the area of a triangle with 3 sides.
| 1. | Area of Triangle with iii Sides Formula |
| 2. | Proof of Area of Triangle with iii Sides Formula |
| 3. | FAQs on Area of Triangle with 3 Sides |
Area of Triangle with three Sides Formula
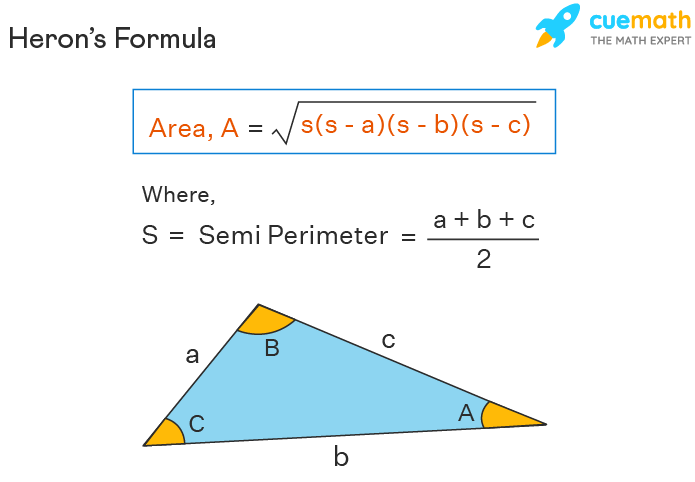
In order to find the expanse of a triangle with 3 sides, we use the Heron's formula which says if a, b, and c are the three sides of a triangle, then its area is,
Area = √[s(s-a)(s-b)(s-c)]
Here, "s" is the semi-perimeter of the triangle, i.e., s = (a + b + c)/2.
Permit the states run into how to find the expanse of a triangle with 3 sides given as: iii, 6, and vii. We know that a = 3, b = 6, and c = 7, the semi-perimeter is, s = (a + b + c)/ii = (3 + half dozen + 7)/ii = eight. Nosotros will find the area of the triangle using the Heron's formula.
A = √[southward(s-a)(southward-b)(s-c)]
= √[8(8-3)(8-half dozen)(8-7)]
= √[8 × 5 × 2 × 1]
= √(80)
≈ 8.94
Proof of Area of Triangle with 3 Sides Formula
The proof of the formula for the area of triangle with 3 sides can be derived in the post-obit way.
Consider the triangle shown above with sides a, b, c, and the opposite angles to the sides every bit bending A, angle B, angle C.
Using law of cosines, cos A = (btwo + c2 - aii) / 2bc.
Using one of the Trigonometric identities,
sin2 A = one - cos2 A
\( \begin{align}\sin A &= \sqrt{i-\cos^2A}\\[0.2cm]\sin A &= \sqrt{1 - \dfrac{(b^2+c^ii-a^2)^ii}{4b^2c^2}} \\[0.2cm] \sin A &= \dfrac{\sqrt{4b^2c^2 - (b^2+c^2-a^2)^2}}{2bc} \\[0.2cm] \dfrac{i}{ii} bc \sin A& = \dfrac{\sqrt{4b^2c^two - (b^2+c^2-a^ii)^2}}{4} \end{align}\)
Nosotros know that one of the formulas of the area of a triangle is ½ bc sin A. Thus, the area of triangle = \(\dfrac{\sqrt{4b^2c^2 - (b^two+c^2-a^2)}}{4}\).
Now, we will derive Heron's formula using the above formula just by applying some algebraic techniques. The higher up formula tin can be written as:
\( \begin{align} &\text{Surface area }\\[0.2cm] &= \dfrac{\sqrt{(2bc)^2- (b^ii+c^2-a^ii)^two}}{4}\\[0.2cm] &= \dfrac{1}{four} \sqrt{[ (b^2+c^two+2bc) - a^2] [ a^2 - (b^2+c^ii-2bc)}\\[0.2cm] &= \dfrac{i}{4} \sqrt{[ (b+c)^2-a^ii] [a^two-(b-c)^2]}\\[0.2cm] &= \dfrac{1}{four} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}\\[0.2cm] \finish{align} \)
We know that the semi-perimeter of a triangle is, s = (a + b + c)/2. From this,
a + b + c = 2s
b + c - a = 2s - 2a
a + b - c = 2s - 2c
a - b + c = 2s - 2b
Substituting all these values in the final step,
\( \brainstorm{marshal}& \text{Area } \\[0.2cm]&= \dfrac{1}{4} \sqrt{2s (2s-2a)(2s-2c)(2s-2b)}\\[0.2cm] &= \dfrac{iv}{four} \sqrt{southward(s-a)(s-c)(s-b)}\\[0.2cm] &= \sqrt{due south(s-a)(s-b)(s-c)} \terminate{align}\)
Hence, we proved the Heron's formula.
Solved Examples on Area of a Triangle With three Sides
go to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer exist a tough subject, especially when yous understand the concepts through visualizations.
Book a Free Trial Course
Practice Questions on Area of a Triangle With 3 Sides
go to slidego to slide
FAQs on Surface area of Triangle with 3 Sides
What is the Area of a Triangle With three Sides?
The expanse of a triangle with 3 sides can exist calculated with the help of the Heron's formula according to which, the area of a triangle is √[s(s-a)(s-b)(due south-c)], where a, b, and c, are the iii unlike sides and 's' is the semi perimeter of the triangle that tin can exist calculated as follows: semi perimeter = (a + b + c)/2
What is the Surface area of Triangle with 3 Sides Equal?
If a triangle has 3 equal sides, it is called an equilateral triangle. The expanse of an equilateral triangle can exist calculated using the formula, Surface area = atwo(√3/4), where 'a' is the side of the triangle. For example, if an equilateral triangle has a side of 6 units, its area volition be calculated equally follows. Area = a2(√3/4), Area = half-dozen2(√iii/4) = 15.59 square units.
What is the Area of Triangle with 3 Sides and Height?
If we know the sides of a triangle along with its superlative, we can use the basic formula for the expanse of a triangle. Expanse of a triangle = 1/two × base × peak. For example, if the height (altitude) of a triangle = viii units, and the side of the triangle on which the altitude is formed is given (base) = 7 units, we can detect its area using the formula, Area of a triangle = one/2 × base of operations × acme. Area = 1/2 × 7 × eight = 28 square units.
What is the Area of a Triangle with three Sides and an Angle?
If the sides of a triangle are given forth with an included angle, the area of the triangle tin be calculated with the formula, Area = (ab × sin C)/2, where 'a' and 'b' are the 2 given sides and C is the included angle. This is also known equally the "side angle side " method. For example, if ii sides of a triangle are v units and 7 units and the included bending is sixty°, then, Area = (seven × 5 × sin 60)/2 = fifteen.xv foursquare units.
What is the Area of a Triangle with Sides 3, 5, 7?
If the three sides of a triangle are given as iii, 5 and 7, its area can be calculated with the formula, area = √[southward(s-a)(s-b)(due south-c)]. In this example, a = 3, b = 5, c = seven, and due south (semi perimeter) = vii.five. Substituting the values in the formula, √[seven.5(7.5-3)(7.5-five)(seven.5-7)] = √(7.5 × 4.v × 2.5 × 0.v) = 6.49 unittwo
What is an Irregular Triangle?
An irregular triangle is a triangle in which all 3 sides are of unlike lengths. It is as well known equally a scalene triangle (if all three sides are different).
How do you find the Area of an Irregular Triangle?
Nosotros employ the Heron'southward formula to find the area of an irregular triangle. An irregular triangle means a triangle whose sides are dissimilar in length. Co-ordinate to the Heron'due south formula: Area = √[s(s-a)(s-b)(south-c)], where, a, b and c are the sides of the triangle, and 's' is the semi perimeter of the triangle.
How to Find the Length of the sides of a Triangle with 3 Angles Only?
Let u.s.a. recall the fact that two similar triangles have the aforementioned angles just different sides (sides are in proportion). Thus, in that location are an infinite number of triangles with the same prepare of whatsoever 3 given angles. So information technology is not possible to find the sides of a triangle if we but know all three angles, we need to know at least one side to make up one's mind the other two sides.
What is Heron's Formula Used For?
Heron's formula is used to find the area of a triangle that has iii dissimilar sides. The Heron's formula is written as, Area = √[southward(due south-a)(s-b)(s-c)], where a, b and c are the sides of the triangle, and 's' is the semi perimeter of the triangle.
Who is Heron's Formula Named Subsequently?
Heron's formula is named after the Heron of Alexandria, a Greek mathematician, who plant the area of a triangle using the 3 sides. That is the reason why the formula √[s(s-a)(s-b)(s-c)] is known as the Heron's formula.
Source: https://www.cuemath.com/measurement/area-of-triangle-with-3-sides/
Postar um comentário for "How to Know if You Can Have a 3rd Leg of a Triangle"